下一个排列

约 473 字大约 2 分钟

2024-12-13

⭐️ 题目日期：

字节 - 2024/11/20，字节 - 2024/9/24

🌳 题目描述：

整数数组的一个排列就是将其所有成员以序列或线性顺序排列。

例如，arr = [1,2,3] ，以下这些都可以视作 arr 的排列：[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。

整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地，如果数组的所有排列根据其字典顺序从小到大排列在一个容器中，那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列，那么这个数组必须重排为字典序最小的排列（即，其元素按升序排列）。

例如，arr = [1,2,3] 的下一个排列是 [1,3,2] 。
类似地，arr = [2,3,1] 的下一个排列是 [3,1,2] 。
而 arr = [3,2,1] 的下一个排列是 [1,2,3] ，因为 [3,2,1] 不存在一个字典序更大的排列。

给你一个整数数组 nums ，找出 nums 的下一个排列。

必须原地修改，只允许使用额外常数空间。

示例1：

示例 1：
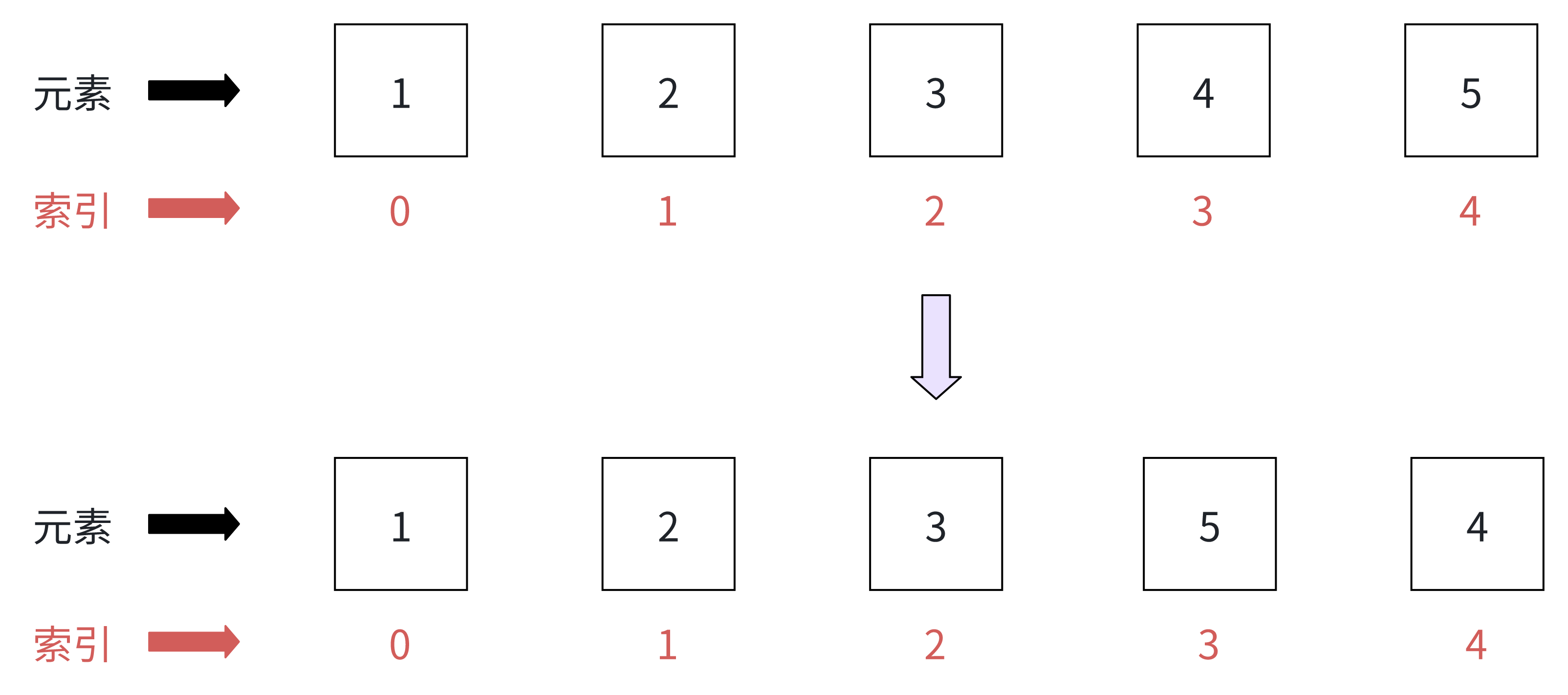
输入：nums = [1, 2, 3, 4, 5]
输出：[1, 2, 3, 5, 4]

解释图例：

🕵🏽 面试评估：

这道题考察候选人是否熟悉字典序排列的概念，是否能理解“从右向左遍历寻找升序对”和“局部最小调整”的核心思想，且能否熟练应用双指针方法来完成交换和反转操作。

🧗难度系数：

⭐️ ⭐️ ⭐️ ⭐️

提示