外观
二叉树的遍历
⭐️ 题目日期:
字节 - 2025/1/4,小米 - 2024/10/10,百度 - 2024/8/13
🌳 题目描述:
二叉树的遍历分为:
前序遍历:先访问根节点,然后遍历左子树,最后遍历右子树。
中序遍历:先遍历左子树,然后访问根节点,最后遍历右子树。
后序遍历:先遍历左子树,然后遍历右子树,最后访问根节点。
记忆小技巧:
前序,中序,后序说的是根节点何时遍历;前序:根节点先;中序:根节点“居中”;后序:根节点最后;
左节点始终先于右节点
实现二叉树的遍历通常有两种方法:递归和迭代,下面我们分别看看这两种方法。
1. 使用递归法实现二叉树的遍历
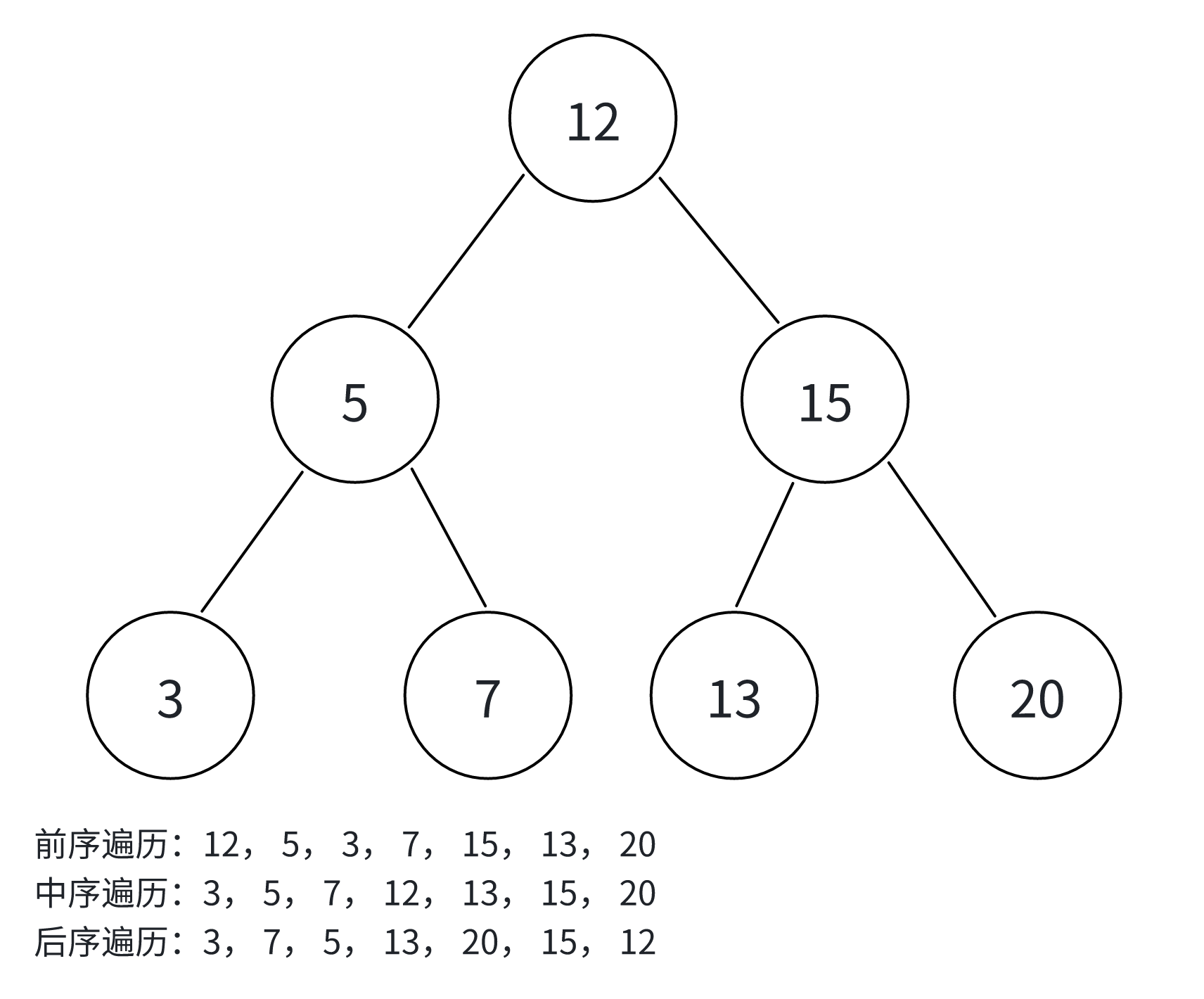
如图所示,二叉树的前序遍历,即(根左右),得到的遍历顺序为:12,5,3,7,15,13,20;中序遍历(左根右),得到的遍历顺序为:3,5,7,12,13,15,20;后序遍历(左右根),得到的顺序为:3,7,5,13,20,15,12
🕵🏽 面试评估:
这道题考察二叉树的遍历方式,即前中后序的递归遍历方式,主要考察候选者能否有效地运用递归思维,将其与二叉树的结构特点结合,完成不同遍历方式的实现。
🧗难度系数:
⭐️ ⭐️
