外观
验证二叉搜索树
⭐ 题目日期：
虾皮 - 2025/4/2，京东 - 2025/3/26，百度 - 2024/9/5
🌳 题目描述：
判断一棵二叉树是不是有效的二叉搜索树
二叉搜索树：
- 节点的值都 大于 其左子树所有节点的值
- 节点的值都 小于 其右子树所有节点的值
- 所有左子树和右子树自身必须也是二叉搜索树。
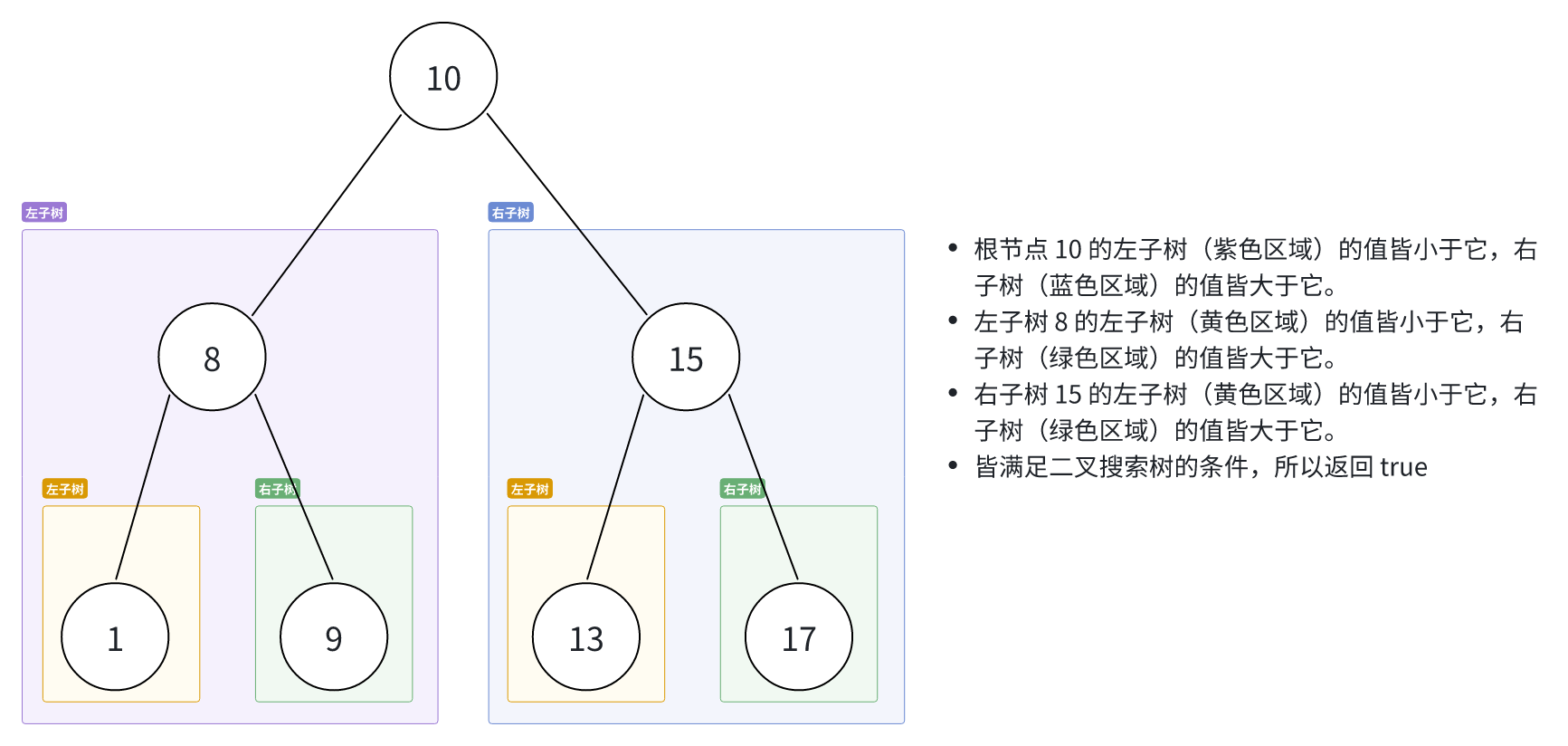
示例 1：
输入：root = [10, 8, 15, 1, 9, 13, 17]
输出：true
解释图例：
示例 2：
输入：root = [10, 8, 9]
输出：false
解释图例：
🕵🏽 面试评估：
这道题考察候选人对二叉搜索树（BST）性质的理解，并且要求候选人能够使用递归或迭代方法（如中序遍历）来检查二叉树是否符合二叉搜索树的规则，并通过适当的边界值（例如，子树值的上下限）来验证每个节点是否符合二叉搜索树的要求
🧗难度系数：
⭐️ ⭐️ ⭐️