外观
重排链表
⭐ 题目日期：
美团 - 2025/3/28, /快手 - 2024/12/13, 百度 - 2024/10/19
🌳 题目描述：
给定一个单链表 L 的头节点 head ，单链表 L 表示为：
L(0) → L(1) → … → L(n - 1) → L(n)
请将其重新排列后变为：
L(0) → L(n) → L(1) → L(n - 1) → L(2) → L(n - 2) → …
不能只是单纯地改变节点内部的值，而是需要实际的进行节点交换。
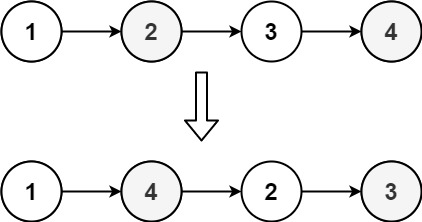
示例 1：
输入：head = [1,2,3,4]
输出：[1,4,2,3]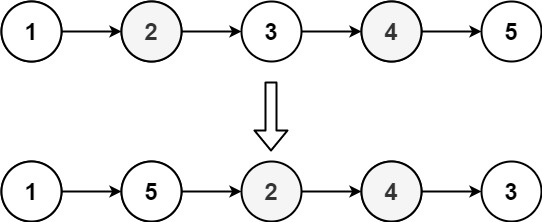
示例 2：
输入：head = [1,2,3,4,5]
输出：[1,5,2,4,3]🧗难度系数：
⭐️ ⭐️ ⭐️️ ⭐️