外观
合并区间
⭐ 题目日期:
华为 - 2024/12/3,字节 - 2024/9/29
🌳 题目描述:
一个大列表里面包括若干个包括两个整数的小列表,如 [[1, 2], [3, 6], [4, 7]],每个小列表代表一个范围 [start, end] ,合并其中重叠的范围并输出。
示例 1:
输入:intervals = [[1, 2], [3, 6], [4, 7]]
输出:[[1, 2], [3, 7]]解释图例: 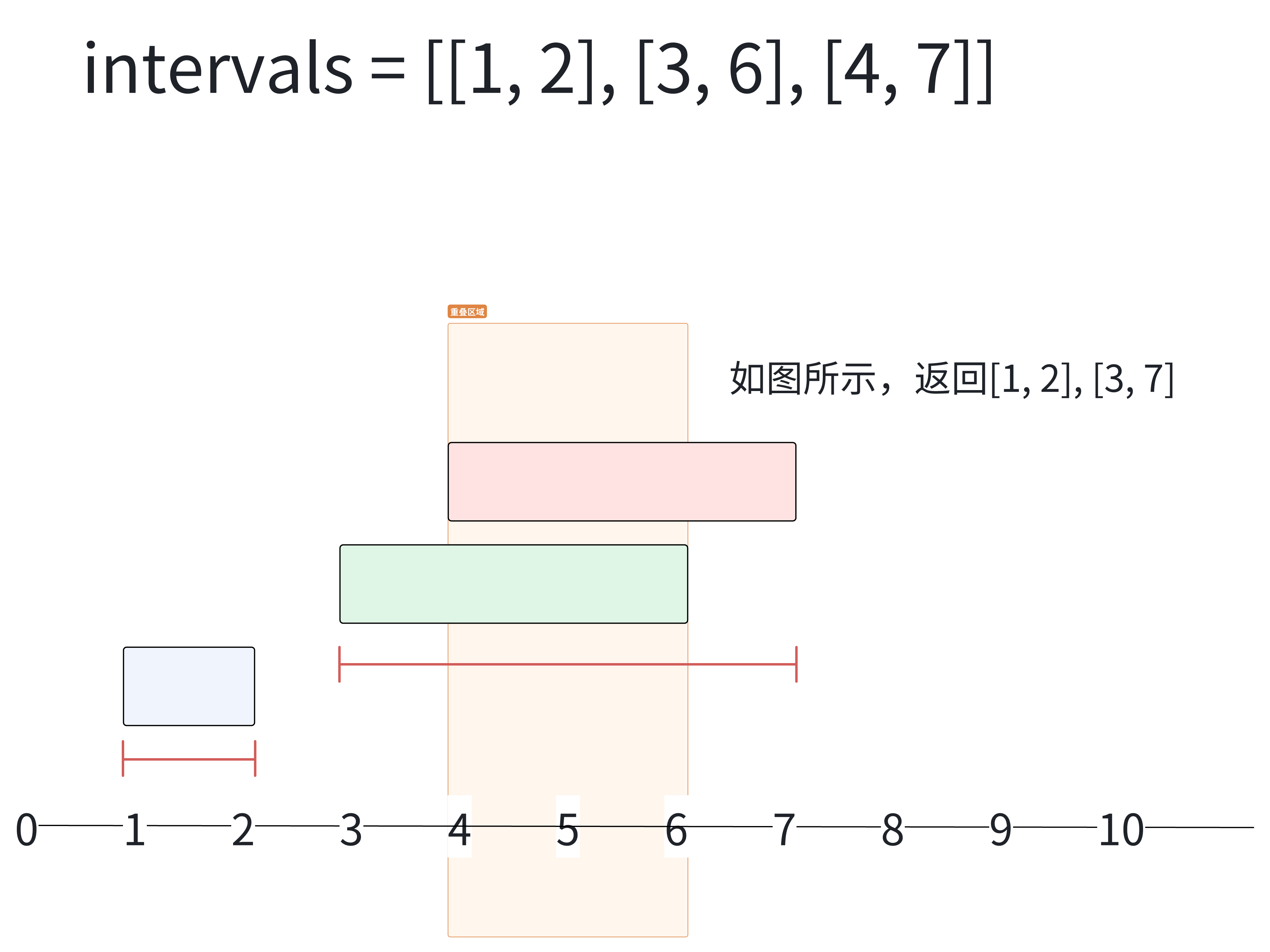
🕵🏽♂️ 面试评估:
这道题主要是考察候选者是否能首先认识到要进行排序操作来方便后续的合并,是否能够正确应用排序算法来对区间进行排序,并使用双指针策略来合并区间。
🧗难度系数:
⭐️ ⭐️ ⭐️
