使用两个栈实现队列

约 204 字小于 1 分钟

2024-12-12

⭐ 题目日期：

腾讯 - 2024/12/20,2024/8/19

🌳 题目描述：

使用两个栈实现队列，支持 poll，offer，peek 操作；队列：按照先进先出的原理运作，在队尾加入元素，在队头弹出元素

示例 1：
输入：["MyQueue", "offer", "offer",  "offer", "offer","peek", "poll","peek"]
[[], [1], [3], [2], [4], [], [], []]
输出：[null, null, null, null, null, 1, 1, 3]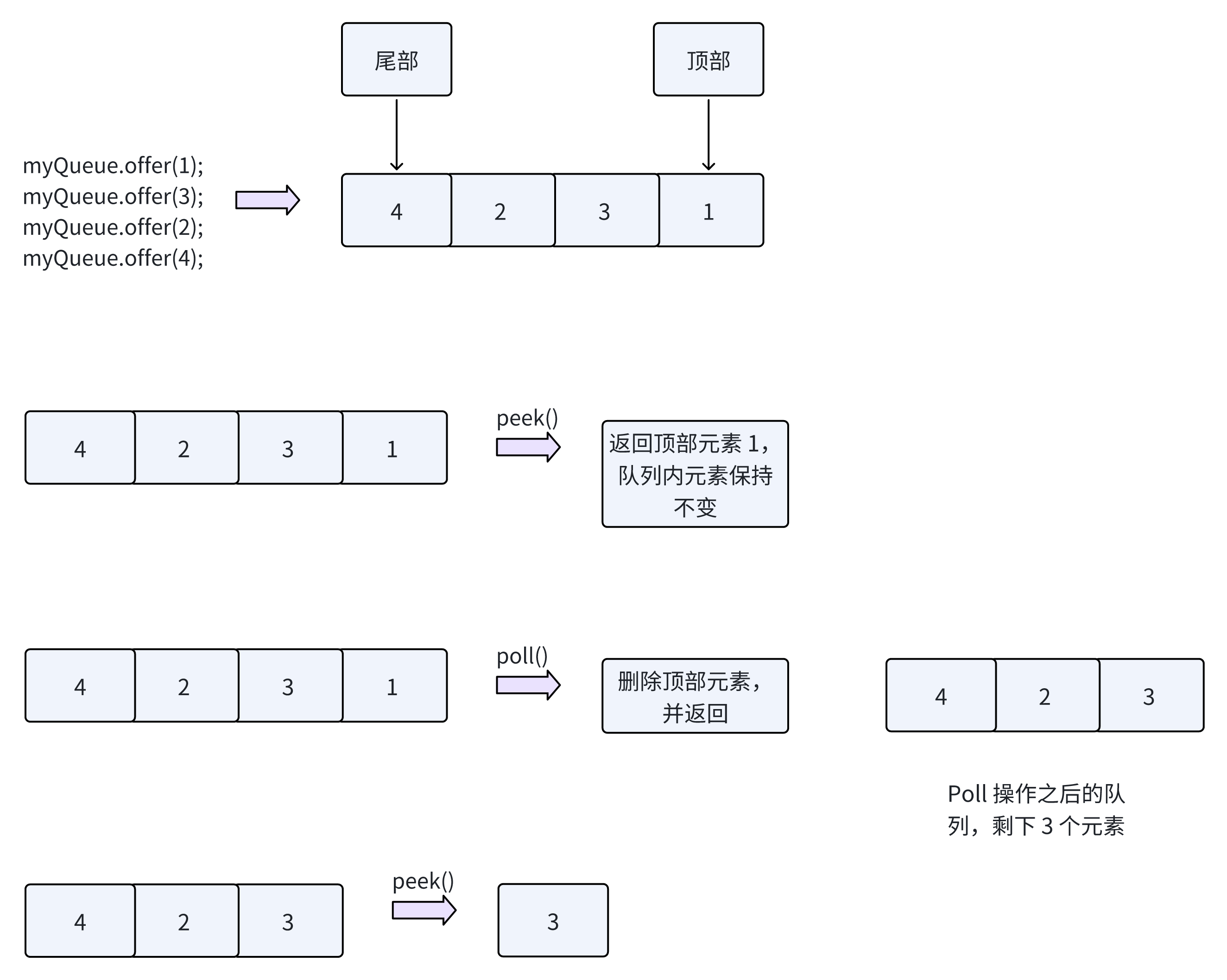

🕵🏽 面试评估：

这道题考察候选人对队列先进先出特性的理解，能否结合栈的特性模拟队列，且能够正确处理边界条件（如空队列时的返回值）。

🧗难度系数：

⭐️ ⭐️

提示